立志欲坚不欲锐,成功在久不在速
leetcode
原地算法基本就是:双指针加反转。
必会知识点
原来如此,既然ArrayDeque是双端队列,那我如果只对一端进行操作那不就变成了栈了,管它是队列头还是队列尾,也就是说如果想当成栈操作,则各个操作要在同一端
比如 peek、pop、push、poll都在队列头部操作 getLast、removeLast、offer/add都在队列尾部操作 所以这两种方式都可以模拟成栈
PriorityQueue<int[]> queue = new PriorityQueue<>((o1, o2) -> o1[0]-o2[0]); // 这样的话就是小根堆
int[][] prerequisites, Arrays.sort(prerequisites, (o1, o2) -> o1[0]-o2[0]);
通过调用 Arrays.sort(prerequisites, (o1, o2) -> o1[0] - o2[0]);,你正在对二维数组 prerequisites 进行排序。具体来说,它会按照每个子数组(即 prerequisites 中的每一个一维数组)的第一个元素(o1[0] 和 o2[0])进行升序排序
PriorityQueue 默认是最小堆,Comparator (a, b) -> a - b 也会导致元素以升序排列。
红黑树好文
左旋:选择一个pivot节点,其父节点(root)左旋为自己的左子树,然后自己的原左子树变为原root节点的右子树,其他不变。(能这样旋转说明pivot原先是root的右子树,也就是右边高度太大了)
右旋:选择一个pivot节点,其父节点(root)右旋为自己的右子树,然后自己的原右子树变为原root节点的左子树,其他不变。(能这样旋转说明pivot原先是root的左子树,也就是左边高度太大了)
在 Java 中,所有的整数都是以二进制「补码」的形式存储的(PS:正数补码是本身,负数补码是对应正数带上符号位一块取反,然后加一)
比如-2^31是1000….000,实际上就是最高位(第32位的1,也即符号位1)本身就是代表-2^31,所以后面我们想要哪些负数,就在这个基础上加”正数”就好了,比如我加一个2^31-1即0111…111,那就得到了-1即1111…111。
在 Java 中,>> 是「带符号右移」操作符,它会将所有位向右移动指定的位数,「左边」空出的位「用原来的符号位」填充。这里注意:假如一个负数右移十位,实际上是在左边补了10个1。
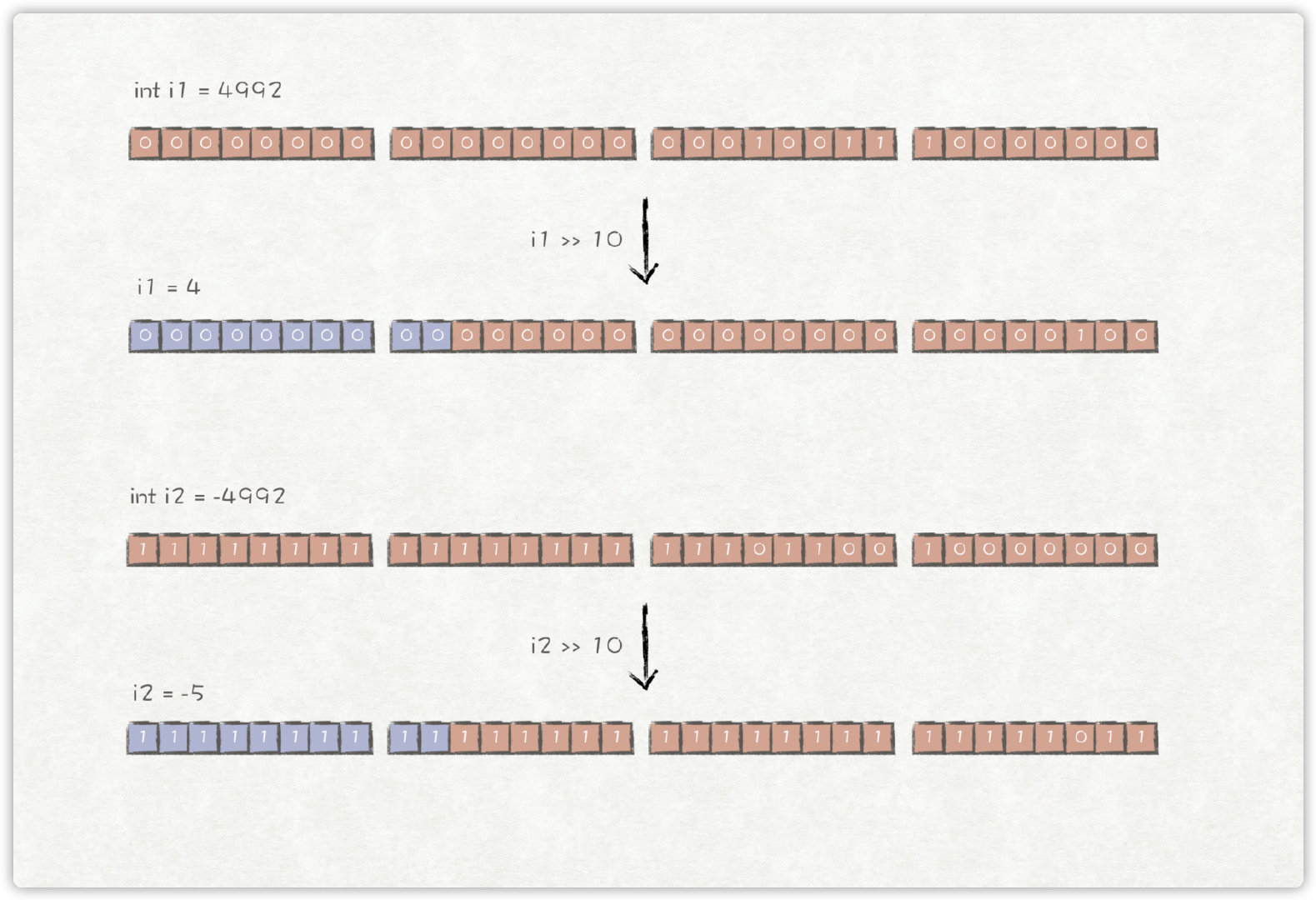
在 Java 中,>>> 是无符号右移操作符,它会将所有位向右移动指定的位数,左边空出的位用 0 填充,不论原来的数是正数还是负数。
数组
二维数组用的时候不能直接push_back()一个元素,要往某一维上push一个元素先要往这个二维数组里push一个一维数组,like this:ret.push_back(vector <int> ());
或者先建立一维数组来存放值,再push进二维数组。
或者动态resize二维数组的大小。
n数之和
经典题,用哈希表会非常难写,虽然也可以做到O(n^2)的时间复杂度,但是很难去重。
这题比较好的解法是排序加双指针,排序后的双指针非常好用。
912 排序数组
经典排序题
复习基础排序算法
这篇题解写的非常好,将排序算法讲的很通透。
二分查找
来一波二分查找的总结吧。
二分查找有两种题(目前做到的)
第一种:你的目标一定存在,你一定能找到唯一一个数符合你的目标,比如374. 猜数字大小 这种题随便写,可以用我后面重点说的通用解法,也可以用在循环里分(<、>、 ==)三种情况,都很好写。
第二种题:你的目标不一定存在,你可能要找你的理论目标最近的一个数,可能是 小于等于target的最大数 或 大于等于target的最小数。比如35. 搜索插入位置、278. 第一个错误的版本、 69. x 的平方根、(注:这种平方题可以用二分迭代法做)367. 有效的完全平方数 等都是要找离目标最近的数,并且大多数不止要让你返回 true or false,还要你返回索引。
接下来重点介绍通用二分模板:
以367. 有效的完全平方数 为例:
1 | long low = 0, high = 1<<16, mid = 0; |
首先,用 mid=(low+high)/2 可以,但是用 (high-low)/2+low 更好(这俩是一模一样的),因为 (low+high) 可能超出 int 的范围。
其次,用 while(low<high) 更好。根据这里我们可以找第一个平方大于等于目标数的数(当然也可以找最后一个平方小于等于目标数的数),并且注意到(mid*mid>=num) high = mid 也就是说high始终有可能就是第一个平方大于等于目标数的数,而(mid*mid<num)是mid很明显不是我们想要的,所以我们让low = mid+1,能不能让low=mid也不动,绝对不行!因为这里的mid已经确定不符合题意,一定要有一个逼近的过程,即使逼近程度只有1,否则等low high很接近的时候一定会死循环。
这样有什么好处?我的目标就是,始终让第一个平方大于等于目标数的数就在[low,high]中间,这里是闭区间,那么当low==high的时候左右两区间重合就可以自动退出循环,并且low or high就是我们想要的,后续所有的判断都可以根据这两个数来。这里又体现一个好处,退出循环的时候一定是low==high(因为两个数加起来一次循环也只会变化1),如果用的是 while(low<=high)退出的时候还要去想诶,到底low or high or mid哪个是有价值的数据,很折磨的。
还有一个很重要的问题,如果我找最后一个平方小于等于目标数的数,是不是只需要修改以下两个关键语句就可以呢?也就是:
1 | while(low<high) { |
错误!为什么?
细想,当low high 只差1的时候,mid是不是等于low,如果此时的low*low<=num是不是死循环了,low又等于mid,mid永远等于low,high根本没判断过呢,万一high才是最后一个平方小于等于目标数的数呢。
所以关键就是:low可能不动,所以要让mid去等于high(当然是low high 只差1的情况),也就是得这样mid = (high-low+1)/2+low;
1 | while(low<high) { |
总结下来:low和high中一个不动,计算mid的时候一定要等于另一个,不然low high相邻的时候就会死循环。
目前来看,所有二分查找都可以用这个模板,灵活变通吧。
多数元素
169. 多数元素
被简单题薄纱(加进阶是真难)
这题有很多解法:随机化(第一次见这种抽象解法)、分治、Boyer-Moore 投票算法
分治的关键在于:将数组分成两个子数组之后,数组的主要元素一定是两个子数组主要元素之中的一个,因为如果数组的主要元素不是两个子数组主要元素之一,那这个主要元素出现次数一定小于数组一半(反证法)。
分治法还要考虑到最小子问题才能成型,也就是长度为1的数组的主要元素就是其中唯一的数。
分支法还能解决问题:数组中出现次数最多的数字,不会受到题目中的限制(超过半数)。
merge过程中都是要再遍历一次数组的,两个子问题加上n,总的时间复杂度就是O(nlgn)。
Boyer-Moore 投票算法:同归于尽消杀法
448. 找到所有数组中消失的数字
448. 找到所有数组中消失的数字
利用数组当哈希表(原地),巧妙利用数据的宽度,结合取模在保有原数据信息的同时加入了新的信息。
4. 寻找两个正序数组的中位数
二分查找 真的难 写不出来。二分简单,但关键是怎么把问题抽象成二分,像这题转换为找第K数,然后每次减半,我就没想到这个转换,麻了。
二分法我思路差不多呀,但我想的是大的那个数的右边也要删,两边都删然后向中间靠拢,然后破防了太难整了。转换成第K数真的太关键了。
1 | class Solution { |
数学
计数质数
位运算
位运算很重要,有些题很有技巧性
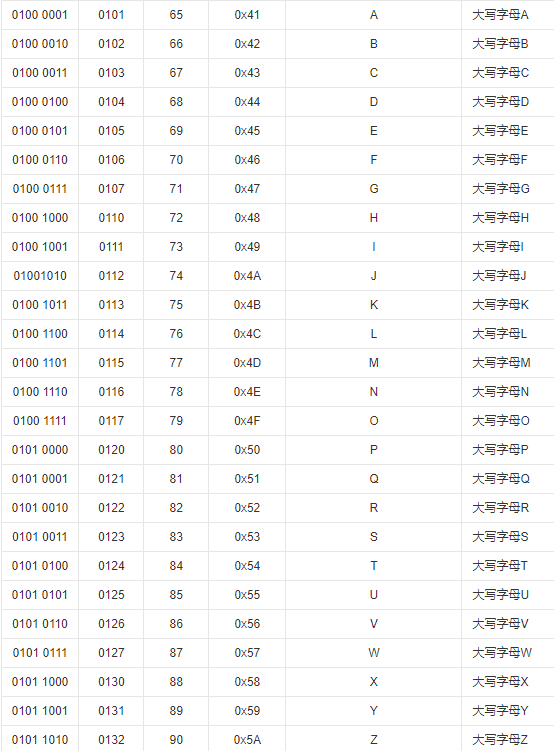
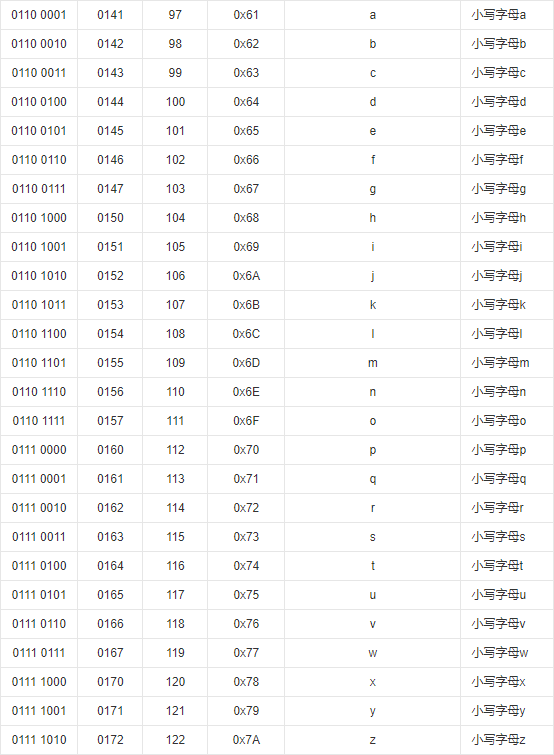
注意观察规律,A 到 Z 的低六位是 1 到 26,也就是 000001 到 011010。
而 a 到 z 的 低六位 是 33 到 58,也就是 100001 到 111010。
相差刚好是 倒数第六位的二进制 1 ,也就是 32(97-65),应该ascii码就是这么设计的,这样的话 (A |= 1<<5)==a,| 运算在这里等效于加法。
并且 A 到 Z 、a 到 z 的 低六位各不一样,分布在 1 到 64内,可以直接用 一个64bit 的long型整数压缩存储A 到 Z 、a 到 z,如:771. 宝石与石头
1 | char ch; |
这样每个 A 到 Z 、a 到 z 都可以用 mask 的 1 bit 来存储。
上面提到的两种用法都是在题里面见到过的。
只出现一次的数字
对于这道题,可使用异或运算 ^。异或运算有以下三个性质。
任何数和 0 做异或运算,结果仍然是原来的数。
任何数和其自身做异或运算,结果是 0。
异或运算满足交换律和结合律。
137. 只出现一次的数字 II
这题是真难。
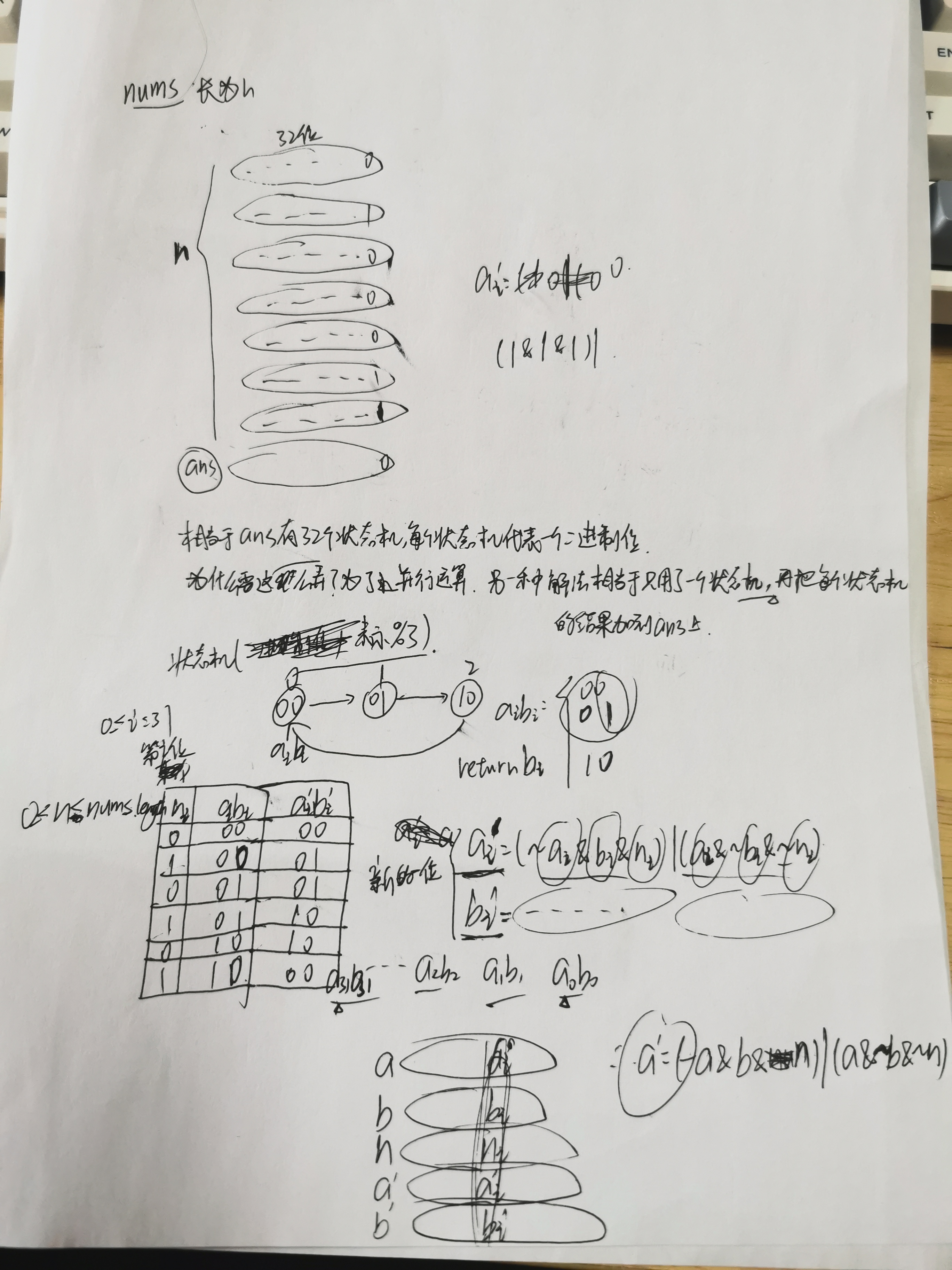
其实关键就是:数电的方法优化在利用位运算的并行性,直接使用32个状态机(每个二进制位都当作一个状态机),而方法二只使用了一个状态机,所以时间复杂度多了一个logC。
二进制求和
两个二进制数 异或^ 可以视作忽略进位的求和,但之后要补上进位。
怎么补呢?用 与& ,&完之后还需要左移一位(能理解吧),之后迭代重复以上步骤直到进位变为0。
同时注意:java里数字异或不需要转为二进制数,用十进制数来异或是正确的。
Integer.parseInt(String 2)将字符串a按二进制解析其内容(解析成10进制数),Integer.toBinaryString(int n)将十进制数转为二进制字符串。
颠倒二进制位
190. 颠倒二进制位
这个分治解法太骚了,翻转一个二进制串,可以将其均分成左右两部分,对每部分递归执行翻转操作,然后将左半部分拼在右半部分的后面,即完成了翻转。
上面的是正常解法,是自顶向下的。
但是,注意到位运算的特殊性,并且左右两边的计算方法相同,并且已知是32位的二进制数,所以我们可以直接自底向上(到这里总算开始理解了自底向上,其实自底向上并不总是用在递归中,用在这里或者用在动态规划就像作弊一样,关键点就在你要知道底在哪里,并且向上的过程要很清楚)。
这里直接定义4个常数M1234,他们的意思分别就是最后一层(只颠倒奇偶)、倒数第二层(将颠倒奇偶之后的按两位一组分成奇偶组,接着颠倒奇偶组)、倒数第三层、倒数第四层。
另外注意的是,在某些语言(如Java)中,没有无符号整数类型,因此对 n 的右移操作应使用逻辑右移 >>>。
同样的分治解法还有数1的个数191. 位1的个数
4的幂
342. 4的幂n & (n - 1)==0 判断 n 是否是 2 的幂,==0就是2的幂,2 的幂是一个很严格的条件。5*2^6并不是2的幂,2的幂和4的幂真的就差一点,补充条件即可。
2的幂
一个数 n 是 2 的幂,当且仅当 n 是正整数,并且 n 的二进制表示中仅包含 1 个 1。
因此我们可以考虑使用位运算,将 n 的二进制表示中最低位的那个 1 提取出来,再判断剩余的数值是否为 0 即可。下面介绍两种常见的与「二进制表示中最低位」相关的位运算技巧。
关键就是只管最低位的1。
n & (n - 1)==0 注意,n = n & (n - 1)操作可以将任意整数 n 的最后一位1变为0,由于2的幂只有一位1,所以最后一位1变为0之后结果如果是0则n为2的幂。
n & (-n)==n 能够直接提取最低位的1,其他位都变为0。
那么 n 就是 2 的幂。
还有剑招:用2的最大幂除n,能整除则true。
比特位计数
338. 比特位计数 有库函数法(Integer.bitCount())、动态规划解法,也可以用Brian Kernighan 算法,原理就是利用前面说过的n = n & (n - 1)操作可以将任意整数 n 的最后一位二进制 1 变为 0 ,那么对 x 重复该操作,直到 x变成 0,则操作次数即为 x 的「一比特数」。
错误的集合
这个位运算解法还不错,
链表
环形链表2
哈希表
unordered_set<ListNode *> visited;
unordered_set可以用 ListNode * 数据类型
快慢指针一定在环内相遇,根据数学来找到开始入环的第一个节点。
Floyd 判圈算法
Floyd判圈算法(Floyd Cycle Detection Algorithm),又称龟兔赛跑算法(Tortoise and Hare Algorithm),是一个可以在有限状态机、迭代函数或者链表上判断是否存在环,以及判断环的起点与长度的算法。
160. 相交链表
被简单题薄纱(没有题感说实话)
相交链表
148. 排序链表
自底向上归并排序(用迭代不用递归),第一次见归并竟然没用递归然后做到了O(1),真牛啊自底向上。
难哟。
以后可以尝试写一下,其实思路和递归归并是一样的,不过要在循环里控制长度sublength进行手动分组,记得分组完要切断其与前后的联系,相当于独立出两个小链表,然后合并(O(n)时间和O(1)空间)。
哈希
在字符匹配的题里尽量用数组代替哈希表。这个很重要很重要
哈希表的 value 可以是一个数组,见697. 数组的度
这个用法真的很重要。如java: Map<Integer, int[]> map = new HashMap<Integer, int[]>();
在实际代码中,我们使用哈希表实现该功能,每一个数映射到一个长度为 3 的数组,数组中的三个元素分别代表这个数出现的次数、这个数在原数组中第一次出现的位置和这个数在原数组中最后一次出现的位置。
202 快乐数
对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和,然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。如果 可以变为 1,那么这个数就是快乐数。
要找是否存在环(循环)的题都可以用 快慢指针 这种思想。
本题还可以使用哈希表unordered_set。
设计哈希集合
为了实现哈希集合这一数据结构,有以下几个关键问题需要解决:
哈希函数:能够将集合中任意可能的元素映射到一个固定范围的整数值,并将该元素存储到整数值对应的地址上。
冲突处理:由于不同元素可能映射到相同的整数值,因此需要在整数值出现「冲突」时,需要进行冲突处理。总的来说,有以下几种策略解决冲突:
- 链地址法:为每个哈希值维护一个链表,并将具有相同哈希值的元素都放入这一链表当中。
- 开放地址法:当发现哈希值 h 处产生冲突时,根据某种策略,从 h 出发找到下一个不冲突的位置。例如,一种最简单的策略是,不断地检查 h+1,h+2,h+3,… 这些整数对应的位置。
- 再哈希法:当发现哈希冲突后,使用另一个哈希函数产生一个新的地址。
扩容:当哈希表元素过多时,冲突的概率将越来越大,而在哈希表中查询一个元素的效率也会越来越低。因此,需要开辟一块更大的空间,来缓解哈希表中发生的冲突。
质数取模,其实是利用了同余的概念:当元素是个有规律的等差数列时,并且和基数(数组大小)最大公约数不为1时,就会造成哈希映射时冲突变高(数组某些位置永远不会有值)。比如数列0,6,12,18,24,30…,
base为10,取模(0,6,2,8,4,0…)后,放入哈希表中位置将只能在0,2,4,6,8这几个数组位置上;
但我们如果把base取7(数组大小甚至比10小),同样数列取模后(0,6,5,4,3,2,1,0,…),可以分布在哈希表中的0,1,2,3,4,5,6所有位置上;
后续:若x和y的最大公约为z,x和y的最小公倍数就为(xy)/z,很明显,若z为1,也就是俩数的最大公约数为1的时候,那么俩数的最小公倍数就为xy。那么当一个数为质数时,除了其自身的倍数外,其余数和其的最大公约数都将是1,这时,步长选任何数(除了倍数)都可以满足桶的均匀分布。
所以,以取模计算哈希值在桶中的位置是,用一个质数当作基数时可以使得哈希表中每个位置都“有用武之地”。
Hash表为什么需要使用mod素数?
从素数定理出发,我们可以知道素数有如下性质 素数定理:在初等数学中有一个基本定理,任意一个大于1的自然数,要么本身就是质数,要么可以分解为几个质数之积,这种分解本身,具有唯一性
在知道素数的性质后,回过头来看Hash表,我们将元素放在Hash表当中,需要解决的一个问题就是尽量解决冲突。
给出一份实验,结论表明:模数的因子会影响数列的冲突,而且因子越多,冲突的可能性就越大。而素数的因子恰好只有1和其本身,就非常适合用于解决冲突。
比如 2 4 6 8 10 12这6个数,如果对 6 取余 得到 2 4 0 2 4 0 只会得到3种HASH值,6的因子有1,2,6。冲突会很多。如果对 7 取余 得到 2 4 6 1 3 5 得到6种HASH值,而7的因子只有1,7。由3可知,即使1的因子最小,但是在实际中并不用,因为mod1相当于不解决冲突。而初始化的的数组就会非常大。
原地哈希 41. 缺失的第一个正数
41. 缺失的第一个正数 被原地哈希薄纱了,之前也遇到过原地哈希的。也是在数组的值上动手脚让它能够和其他值区分开来,但这题由于数值不限,所以直接把无用的负值置0,然后用取负值做标志位。
Rabin-Karp 算法
有一题字符串的题也用的这个解法,哪题我忘记了,好像是快乐字符串什么的困难题,还有另一题也用这个,所以这是第三次遇到这个解法。
Rabin-Karp 算法将一个序列 S 计算为哈希值,首先指定基数 base(最好是个质数),将序列 S 看作 base 进制的数求得哈希值,为防哈希冲突可以再哈希等等,不过也够用了。由于这个值一般会非常大,因此会将它对另一个素数 mod 取模。
字符串
字符串匹配问题可以多尝试再复制一份母串,可能会有奇效, 如796. 旋转字符串
C++ 中的 String 类
C++ 标准库提供了 string 类类型。
string类提供了一系列成员函数,比如:
1 | 1. append() -- 在字符串的末尾添加字符(单字符也可以) // 也可以使用+和+=运算符对 string 对象执行字符串的连接操作 |
151 翻转字符串里的单词
真的好题,确实难双指针的极致应用
想一下,我们将整个字符串都反转过来,那么单词的顺序指定是倒序了,只不过单词本身也倒序了,那么再把单词反转一下,单词不就正过来了。
O(1)空间复杂度的解法确实想不出来。
整个字符串翻转,再翻转各个单词。思路太难想了吧。
其实想不出来也应该把删除所有多余空格这一步弄出来,一步步做题。之后没准就想出来了。其实还是字符串不熟,没用过erase();
但是erase()是O(n)的时间复杂度,所以不能用。
用前后快慢指针删除vector/string的某一种元素,如果是相向指针会改变顺序,所以得用前后快慢指针来删除空格。
28. 实现 strStr()
KMP算法经典问题, 找字串
1 | void getNext(vector<int>& next, const string& s) { |
KMP算法的前缀next数组最通俗的解释 这篇文章讲的不错。
很重要的一点就是,匹配失败的时候要找已经匹配的字符串内部对称的子字符串,这也是KMP的内核,当一个字符串的对称程度越高,KMP算法效果越好。这里的对称不是指一次对称,而是像这样的:
01234567891011
abtab gabtabt3
00012012345
t无法继承(如果这个字符没有失配,配哪个呢,索引就是前一个字符的next值,那它的next就是前一个字符的next加一)前一个字符的next对应值因为这里失配了,即t=s[i],这时候s[i]不等于s[(k=next[i-1]=next[b]=5)]=g。
那这时候t的next值怎么看,开始找匹配好的字符串里面的子对称字符串,并且t一定要和那个子对称的下一个字符相同。
更新k = next[k - 1]=next[4]=2;这时候的k代表已经匹配好的字符串里的子对称的长度,你看abtab里面的ab。ab就是我们要找的子对称字符串,它的下一个字符是不是t,这时候就匹配了可以退出循环,next[t]=k+1;
那为什么更新k = next[k - 1]呢,这一步挺关键的。
原来的k是5,是什么意思?这个5=next[t-1]是t前一个字符b的next,表示这个字符和它前四个字符也就是长度为5的后缀与长度为5的前缀相同。
那我要找这个匹配好的长为5的字符串的子对称字符串怎么找,那当然是next[4](索引是长度-1)直接查前缀就行。
有更复杂的情况
abtababtab g abtababtabt
00012123450123456789103
这种才是真正的对称
更新k = next[k - 1]你要更新两次才能找到,找到什么?匹配好的字符串里面的子对称字符串,并且t一定要和那个子对称的下一个字符相同。
刚开始:k = 10;
更新:k=next[k-1]=next[9]=5
这不是找到abtababtab长为5的对称子串了吗?但是,这个字串的下一个字符是a,不等于t就,也就是while循环里的判断条件,还得更新。
更新:k=next[k-1]=next[4]=2
这时候终于找到了,所以next[t]=k+1=3;
k=0当然就没意思了,说明没有对称子串了,因为k即next代表相同的前后缀的长度,零的话我直接比较s[i]和s[0](也是s[k])不就好了。
时间复杂度O(m+n),空间复杂度O(m) n是主串长度,m是模式串长度
459.重复的子字符串
上限很高的简单题
要理解一个关键原理:
长度为 n 的字符串 s 是字符串 t=s+s 的子串,并且 s 在 t 中的起始位置不为 0 或 n,当且仅当 s 满足题目的要求(给定一个非空的字符串s,可以通过由它的一个子串重复多次构成。),即为充要条件。
可以用string类自带的find函数查找索引,之所以要求索引不为0或n,是因为第一个删除了s+s的第一个和最后一个”子串”,两个s都不完整,由于子串长度至少大于1,所以删除前后各一个字符。
当然也可以用KMP实现自己的查找函数。
这题还能进一步优化。
符合要求的字符串,最后一位的next值=n-i;
其中n为字符串长度,i为重复的子串的长度。
所以 i = n-next[n-1]
又有gcd(n,i) = i n肯定整除i,并且i为最小的起始位置。
所以只要判断n是否能整除i(n-next[n-1])即可,能整除则true。
队列与栈
匹配问题都是栈的强项。
232 用栈实现队列
就差一点就能更优化,应该再多想想不要急。画个图就能发现,用来输出的第二个栈的元素不用再倒回去。
基本就是输入输出栈完全分开了。
150. 逆波兰表达式求值
这不仅仅是一道好题,也展现出计算机的思考方式
为什么要将看似简单的中缀表达式转换为复杂的逆波兰式?原因就在于这个简单是相对人类的思维结构来说的,对计算机而言中序表达式是非常复杂的结构。相对的,逆波兰式在计算机看来却是比较简单易懂的结构。因为计算机普遍采用的内存结构是栈式结构,它执行先进后出的顺序。
239. 滑动窗口最大值
我用的哈希表加剪枝,以临界时间通过,如果题目数据大一点就不容易通过了。
很难很好的题。
学到很多:优先队列(堆),单调队列(由deque实现,满足单调性的双端队列),通常并不是单独使用的,还有分块加预处理(很有意思的解法,类似稀疏表,其实和线段树有一丢丢像,像53题的线段树也维护最大前缀和、最大后缀和,这里是维护最大前缀最大后缀)。
1 | class Solution { |
数据流中的第 K 大元素 优先队列
小顶堆
直接当普通队列使用即可:
1 | // java |
347. 前 K 个高频元素 优先队列
好题。
优先队列 ,要知道堆的操作时间复杂度是和堆总元素数有关的,如果堆大小至多为k,则每次堆操作需要O(logk)的时间,操作N次的话就是O(Nlogk) 的时间。
还学到了自定义排序规则:
注意定义优先队列的排序时是反过来的,比如>号是小根堆,<号是大根堆。以下的例子都是小根堆,默认创建时为大根堆。
并且注意调用时候的用法
1 | bool cmp(const pair<int, int>& a, const pair<int, int>&b){ |
priority_queue 对象的第一个模板参数是 pair<int, int>,表示队列中的元素类型为 pair。第二个模板参数是 vector<pair<int, int>>,表示使用 vector 作为底层容器。第三个模板参数是自定义的比较函数 cmp 的类型,使用 decltype(&cmp) 来获取函数指针的类型。
读者需要掌握自己实现堆的方法,包括「建堆」、「调整」和「删除」的过程。
可以再看看912排序数组,用了堆排序。
1 | // 大根堆 堆就是完美二叉树并且存储在数组中 |
还有快速选择法(基于快速排序的选择方法),通过每次都只在其中一个分支进行递归,能够将算法的平均复杂度降低到O(N)。
快排可以通过在每次递归的开始随机选取中枢元素来降低出现最坏情况的概率。还可以使用双指针的方法,这种方法可以较好的应对各种数据。
再做一题K大数:
215. 数组中的第K个最大元素
字节真的考过这个,还是得实现O(n)的时间复杂度,所以用堆是不行的。得用快速选择:
根据快排的原理我们知道,在递归一次的时候我们一定可以确定一个元素的最终位置,即 x 的最终位置为 q,并且保证 a[l⋯q−1]中的每个元素小于等于 a[q],且 a[q] 小于等于 a[q+1⋯r]中的每个元素。所以只要某次划分的 q 为倒数第 k 个下标的时候,我们就已经找到了答案。 我们只关心这一点,至于 a[l⋯q−1]和 a[q+1⋯r]是否是有序的,我们不关心。
因此我们可以改进快速排序算法来解决这个问题:在分解的过程当中,我们会对子数组进行划分,如果划分得到的 q 正好就是我们需要的下标,就直接返回 a[q];否则,如果 q 比目标下标小,就递归右子区间,否则递归左子区间。这样就可以把原来递归两个区间变成只递归一个区间,提高了时间效率。这就是「快速选择」算法。
基于快速排序的选择方法
只讨论大量相同的数据的情况,如果只是选择随机数的话是无效选择,基本就是快排的最坏情况即冒泡排序。用双指针版快排则可以有O(nlgn)的时间复杂度因为每次都可以跑到最中间,(顺便说一下,快排有三指针的优化)
1 | int quickselect(vector<int> &nums, int l, int r, int k) { |
注意,双指针是应对大量重复数据的,这也是为什么用 do while ,如果很多数据,则 i j 索引指的数据都相同,这时候 i j 交换完数据后会同时减,这样 i j 碰头的时候基本就在中间,后面只递归一次的时候基本可以少递归一半的重复数组。
树
好难的二叉树( 迭代 递归 都难 )
树的种类
满二叉树
完全二叉树
完全二叉树的定义如下:在完全二叉树中,除了最后一层其它层全部填满,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层(h从1开始),则该层包含 1~ 2^(h-1) 个节点。
优先级队列其实是一个堆,堆就是一棵完全二叉树,同时保证父子节点的顺序关系。
二叉搜索树
前面介绍的树,都没有数值的,而二叉搜索树是有数值的了,二叉搜索树是一个有序树。
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树
(严格递增)
如:
平衡二叉搜索树
平衡二叉搜索树:又被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
C++中map、set、multimap,multiset的底层实现都是平衡二叉搜索树(红黑树),所以map、set的增删操作时间时间复杂度是logn,注意我这里没有说unordered_map、unordered_set,unordered_map、unordered_set,因为它们的底层实现是哈希表。
二叉树的存储方式
链式存储与顺序存储
链式存储方式就用指针, 顺序存储的方式就是用数组。
顾名思义就是顺序存储的元素在内存是连续分布的,而链式存储则是通过指针把分布在各个地址的节点串联一起。
用数组来存储二叉树如何遍历的呢?
如果父节点的数组下标是 i,那么它的左孩子就是 i * 2 + 1,右孩子就是 i * 2 + 2。
二叉树的遍历
二叉树主要有两种遍历方式:
- 深度优先遍历:先往深走,遇到叶子节点再往回走。
- 广度优先遍历:一层一层的去遍历。
DFS
深度优先遍历
- 前序遍历(递归法,迭代法)
- 中序遍历(递归法,迭代法)
- 后序遍历(递归法,迭代法)
前中后序遍历的前中后,其实指的就是中间节点的遍历顺序,只要记住 前中后序 指的就是中间节点的位置就可以了。
中间节点的顺序就是所谓的遍历方式(左子树一定在右子树之前)
- 前序遍历:中左右
- 中序遍历:左中右
- 后序遍历:左右中
这里的左右理解为左右子树更好,同时左右子树也要保持相同的遍历顺序。
做二叉树相关题目,经常会使用递归的方式来实现深度优先遍历,也就是实现前中后序遍历,使用递归是比较方便的。
讲栈与队列的时候,就说过栈其实就是递归的一种实现结构,也就说前中后序遍历的逻辑其实都是可以借助栈使用递归的方式来实现的。
而广度优先遍历一般使用队列来实现,这也是队列先进先出的特点所决定的,因为需要先进先出的结构,才能一层一层的来遍历二叉树。
1 | // 节点定义 |
DFS 递归
1 | // 递归 前序遍历 中序后序同理,修改顺序即可 |
DFS 迭代
二叉树
1 | // 官解的迭代写的真的好 |
1 | // 官解后序 |
N叉树
1 | class Solution { |
1 | // 用 HashSet 标记是否把子节点放进来了,第二次访问才能读取它的 val |
BFS
广度优先一定要想到队列
二叉树层序遍历 也即 广度优先遍历,图的广度优先也是要用队列,出队入队等。
- 层次遍历(迭代法)
需要借用一个辅助数据结构即队列来实现,队列先进先出,符合一层一层遍历的逻辑,而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。
而这种层序遍历方式就是图论中的广度优先遍历,只不过我们应用在二叉树上。
1 | class Solution { |
二叉树的最近公共祖先
体会递归的自顶向下和自底向上
本题时间复杂度是自顶向下(n^2)和自底向上(n)。
自底向上是这样的:要求出当前的值,我先去求子值也即缩小问题规模,不断缩小,再有得出来的一个个小问题的解来构建当前的值并根据题意做出相应的操作。实际上是怎么实现的?那便是二话不说直接往下递归,当然子问题的解你肯定要保留下来,得到了子问题的解边进行你要的操作。放在本题就是:
1 | bool Verify(TreeNode *root, TreeNode* p, TreeNode* q) { |
除了第一句判断root存在否以外,直接就往下递归并保留下子问题的解。
而自顶向下是我往下递归,如果我需要当前问题的解来进行后序的操作,那我一定要现在立刻马上获得,比如这里为了获得flag1 2,我甚至用了Verify这个递归的函数来求解,那肯定带了许多重复运算。那便是O(n^2)。
1 | class Solution { |
我认为自顶向下和自底向上最核心的区别就是自底向上一定先会递归到底再求解问题。而自顶向下不一定会到底(这里考虑的肯定是递归的主函数,而不是Verify),通过在每个节点都立刻算出当前的值,只要问题的解存在,那想必在递归的过程中就已经把问题解决了。
还有一个原因是我没想到可以用全局变量,没必要让递归来返回TreeNode*。
两数之和 IV - 输入二叉搜索树
这题的方法四还是挺厉害的。
具体地,我们对于每个指针新建一个栈。初始,我们让左指针移动到树的最左端点,并将路径保存在栈中,接下来我们可以依据栈来 O(1) 地计算出左指针的下一个位置。右指针也是同理。
计算下一个位置时,我们首先将位于栈顶的当前节点从栈中弹出,此时首先判断当前节点是否存在右子节点,如果存在,那么我们将右子节点的最左子树加入到栈中;否则我们就完成了当前层的遍历,无需进一步修改栈的内容,直接回溯到上一层即可。
实现起来有点像 头尾双指针 遍历 树。
在很多题都可以用,记得在对称二叉树那里也可以用。
两个栈
1 | class Solution { |
另一棵树的子树
难死了
方法一:
深度优先搜索暴力匹配
做两次深度优先,对每个节点的子树做一次暴力匹配。
方法二:深度优先搜索序列上做串匹配
因为一棵子树上的点在 先、中、后序 遍历下是连续的,所以可以判断 串2 是否是 串1 的子串。
我想到这个了,但是,这只是一个必要条件,并不充分。
可以通过引入节点的两个空值 leftNull 和 rightNull 节点来进行标记,这样子串就能唯一匹配。
可以用 KMP 来进行匹配判断。(KMP不知可以用来对字符串进行匹配,也可以用来对数组匹配)
1 | public boolean kmp() { |
方法三: 树哈希
很牛的方法,字节面过要求写出这个,估计是故意为难人的。
自定义哈希函数,把每个子树都映射成一个唯一的数。
本质就是每个子树的哈希值要考虑每个节点的值,子树哈希值,子树大小,以及左右子树拥有不同权值,这样出现冲突的几率比较小。如果还怕出现冲突,可以设计两个哈希函数,由这两个哈希函数生成第三个哈希函数,这就是双哈希。
这里求素数再用上之前学过的 埃氏筛法(此处为欧拉筛)。
回溯
讲道理,遇到回溯题,自己把递归树稍微画一下。
回溯本质就是暴力枚举,通过递归来实现。
尽量多用全局变量(就算集合也可以用全局),可以省内存,但要注意。
不管什么写法(用全局还是传下来的集合参数),添加结果的时候都一定要拷贝一份,不然结果会出错,因为 Java 是 pass by reference。如:ans.add(new ArrayList<>(temp));
1 | // 回溯的第二种经典写法 即:不选走一次,选的话也走一次 |
二进制手表
这是这题的回溯解法,其实就是罗列所有 1 的位数等于 turnedOn 的10位二进制数,进一步判断是否题意( 即 private String convert(int num)中所列的,当不满足时返回空串),所以明确回溯的目标和难点就是罗列所有 1 的位数等于 turnedOn 的10位二进制数(这也是我不会的,毕竟第一次做回溯,后面肯定拿下)。
turnedOn( 1 的总位数 )肯定是关键,分散到十位二进制数的每一位看就是 这一位取0还是取1 的小问题,取了 0,剩余位数一定要满足一共有 turnedOn 个 1 ,取了 1 ,剩余位数一定要满足一共有 turnedOn-1 个 1 ,那很明显了,这就是递归,我们用num保存这个结果传递给两个子递归。剩余 1 的总位数一定要传递,还有个关键就是记录当前走到这个十位二进制数的哪一位了,也就是 参数 idx。
说到递归一定要想到 递归的底是什么,底当然是 turnedOn递减为0,这时候的 数(num) 才能符合第一个要求,这时候就交给private String convert(int num)函数了。
还要注意对回溯剪枝,毕竟回溯是暴力解法,适当的剪枝能提高程序性能,结合我们的
参数 idx 表示走到哪一位了,参数 turnedOn 表示剩余位数还需要取几个1,还有这一定是一个十位二进制数,剪枝呼之欲出:
1 | if ( (turnedOn+idx)>10 ) { |
1 | public List<String> readBinaryWatch(int turnedOn) { |
77. 组合
非递归(字典序法)实现组合型枚举 看不懂,好难
40. 组合总和 II
前提:去重一定要排序。
40. 组合总和 II
第一次做要去重的题,我真的麻了,仅仅是因为不确定局部变量在递归时候的变化(实际上递归时是会进行压栈保存环境的,当你递归出来的时候数据是完全不会变的,看了这么多理论竟然不会用,我真的服了你了),仅仅把preval定成全局的,没有去思考定成局部的数据并付诸行动导致失败,各种尝试都做不出来,离成功就差一点。真的服了你了。
看看人家的:
去重就是,dfs的同一层第二次遍历到一个数,那么就是重复的,保证每一层一种数只会遍历到一次,又因为进入dfs前数组经过了排序(相同数一定相邻),所以去重只需要在每一层遍历一个数时,判断上一个数是否和当前数相同,相同的话就是重复了,就不需要再对这个数进行递归。
1 | class Solution { |
看看我的:
1 | class Solution { |
这题的去重原理可以看 代码随想录
这个去重为什么很难理解呢,所谓去重,其实就是使用过的元素不能重复选取。 这么一说好像很简单!
都知道组合问题可以抽象为树形结构,那么“使用过”在这个树形结构上是有两个维度的,一个维度是同一树枝上使用过(同一子树, 一个子树就是一个集合),一个维度是同一树层上使用过。没有理解这两个层面上的“使用过” 是造成大家没有彻底理解去重的根本原因。
那么问题来了,我们是要同一树层上使用过,还是同一树枝上使用过呢?
回看一下题目,元素在同一个组合内是可以重复的,怎么重复都没事,但两个组合不能相同。
所以我们要去重的是同一树层上的“使用过”,同一树枝上的都是一个组合里的元素,不用去重。其实就是,重复出现的元素,第一次出现的是最好用的,它会把所有有用的集合都包括起来,而后面出现的只会造成重复!
强调一下,树层去重的话,需要对数组排序!
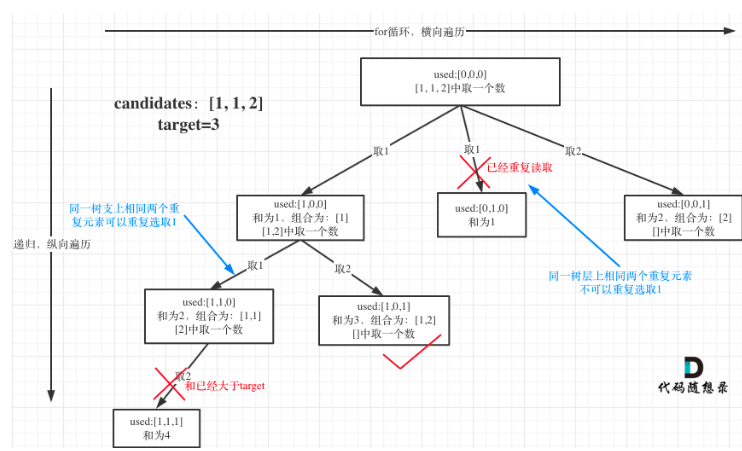
讲道理,遇到回溯题,自己把递归树稍微画一下。
重点在于区分 “树层去重”和“树枝去重”。
妈的还有更狠的:直接用startIndex来去重
1 | class Solution { |
子集 II
注意子集(子序列)和之前的区别,之前是不选没关系,直接往下走就可以,等走到底添加结果,相当于只要叶子节点,而子集在你选或者不选的情况下都需要直接添加进结果,也就是所有节点都是我们想要的结果。
1 | class Solution { |
491.递增子序列
491.递增子序列
真尼玛难啊
这里不能排序了,所以用 hashset uset 表示这层用过的符合要求的数,这里的符合要求指的是非递减。
这种hashset用法也可以用于前面的 子集Ⅱ 题,但是依然需要排序。
比如 4 4 1 4 4 4 不排序的话会有 4 1 和 1 4,那为什么这题不需要排序呢。
因为这题要求非严格递增,不会有 4 1 ,只会有 1 4。
去重题看 代码随想录 讲的确实清楚。
关键还是 树层 不能重复。
唉真是无语了,心累。
46. 全排列
我写了标记数组 ,没想到还有这么秀的解法。
要好好理解递归的变量保存,回溯的撤销操作。
这两点很重要。
撤销撤销撤销
1 | class Solution { |
全排列 II
目前为止已经遇到了 组合、子集、排列的去重。
允许排序的题都可以先排序再去重,当然对这题而言也可以不排序的去重也就是用 uset 记录当前树层使用过的数字,但是之前的组合用 uset 的话也得去重,之前讲过了,这题的话因为是全排列所以可以。
排序去重的话效率肯定更高,这里的话得用标记数组了,不能用之前全排列的优化方法,因为那个方法会改变数字的顺序,排序数组也变乱序数组了。
排序去重最为关键的代码为:
1 | if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) { |
如果要对树层中前一位去重,就用used[i - 1] == false,如果要对树枝前一位去重用used[i - 1] == true。
具体可以看 47.全排列 II中的图。
51. N 皇后
经典回溯,没写出来
37. 解数独
做出来了。
有迭代优化,不断循环固定那些只能放一个数字的位置,之后再去回溯。
494. 目标和
这题最好的做法是转化为0-1背包问题进行求解。
这里说一个回溯的注意事项,困扰了很久。
首先此背包问题可以转化为一个组合问题,关键在于递归的返回时间。
如果用的是 for 循环的写法,不能加上判断索引是否走到数组末尾这个条件,表面上没有影响,实际上是有的,会影响那么几个值,调试一下就知道了,因为如果最后一个数不取也就是不拿(startIndex-1)能达到target,不取之后并没有继续调用递归函数,因为for循环到底了,所以不取最后一个数的结果是没有计入ans的(因为此时startIndex != candidates.length),所以判断不拿是否应该计入ans得在for循环之前判断,而此时startIndex != candidates.length,也就是加入判断索引是否走到数组末尾这个条件确实是会影响的,之前的写法都没有写这个条件所以能通过,之前没注意到这个,没想到今天被暴击了。
并且注意到,反正是组合,达到条件之后自然可以记录下来。
调试果然还是好用的。
1 | class Solution { |
贪心
贪心基本都是 O(n) O(1)
跳跃游戏 II
跳跃游戏 II
有点难,但是能做,迭代有点难看懂。
关键在于:每次选能跳最远的那个位置去跳,别理解成每次跳最远的位置。比如当前位置我能跳到两三个位置,我看从这两三个位置起跳哪个能跳的更远,那这个位置就是局部最优的,当前我就选择跳这个位置。
也就是需要统计两个覆盖范围,当前这一步的最大覆盖和下一步最大覆盖。
每次以最大覆盖范围为一次跳跃次数。
406. 根据身高重建队列
烂题,烂的要死。
没做出来
435. 无重叠区间
没做出来 想死
妈的两题都倒在排序上,没有一点思路,怎么回事啊
我一直想的是移除,实际上反着来才好做,怎样符合题意地去放最多的区间。
我一直找最早下课的,这样我一天才可能上最多的课。
763. 划分字母区间
没用贪心做就是没做出来 , 废物
只要记录最远出现的位置,说实话贪心代码都不太好实现。
1 | int left = 0; |
968. 监控二叉树
这个确实做不来,树dp也看不懂。
这题的后序遍历可以由底至上我知道,输在定义状态,随想录定义了三个状态在进行状态转移真的舒服很多。
定义状态真的很重要啊,像之前的线段树,还有很多动规题,定义出好的状态基本就成功了。
动态规划
状态设计很重要,有时候状态设计是很难看出来的,没有定义状态也就没办法进行状态转移了。
第 300 题:「最长上升子序列」 待做
最后再谈谈状态转移的「无后效性」(当前状态与之后状态无关)
为了保证计算子问题能够按照顺序、不重复地进行,动态规划要求已经求解的子问题不受后续阶段的影响。这个条件也被叫做「无后效性」。换言之,动态规划对状态空间的遍历构成一张有向无环图,遍历就是该有向无环图的一个拓扑序。有向无环图中的节点对应问题中的「状态」,图中的边则对应状态之间的「转移」,转移的选取就是动态规划中的「决策」。
我的解释:
「有向无环图」「拓扑序」表示了每一个子问题只求解一次,以后求解问题的过程不会修改以前求解的子问题的结果;
换句话说:如果之前的阶段求解的子问题的结果包含了一些不确定的信息,导致了后面的阶段求解的子问题无法得到,或者很难得到,这叫「有后效性」,我们在当前这个问题第 1 次拆分的子问题就是「有后效性」的(大家可以再翻到上面再看看);
解决「有后效性」的办法是固定住需要分类讨论的地方,记录下更多的结果。在代码层面上表现为:
状态数组增加维度,例如:「力扣」的股票系列问题;
把状态定义得更细致、准确,例如:前天推送的第 124 题:状态定义只解决路径来自左右子树的其中一个子树。
可以看看这篇讲股票系列问题的动规题解股票问题系列通解(转载翻译)
动态规划的题目分为两大类,一种是求最优解类,典型问题是背包问题,另一种就是计数类,比如这里的统计方案数的问题,它们都存在一定的递推性质。前者的递推性质还有一个名字,叫做 「最优子结构」 ——即当前问题的最优解取决于子问题的最优解,后者类似,当前问题的方案数取决于子问题的方案数。所以在遇到求方案数的问题时,我们可以往动态规划的方向考虑。
判断子序列
392. 判断子序列
判断 s 是否是 t 的子序列。
本质就是对 s 中每一个字符,在 t 中寻找下一个匹配字符,这也是时间复杂度的主要来源,当要匹配的子串 s 很多的时候,重复工作很多,所以可以尝试用动态规划的思想对母串 t 做预处理。
我们可以预处理出对于 t 的每一个位置(0~t.length-1),从该位置开始往后每一个字符(a,b,c,…,z)第一次出现的位置(只需要记录第一次出现的位置即可,不需要更新也不能更新),所以预处理数组dp[t.length][26]是一个二维数组。
令 dp[idx][c] 表示从 idx 位置开始字符 c (也就是当前匹配到的s中的字符)第一次出现的索引,状态转移是:
如果 dp[idx] 处的字符就是 c ,则 dp[idx][c] = idx ,否则 dp[idx][c] = dp[idx+1][c],因为 c 没在 idx 位置,那么 c 一定在 (idx+1) 位置或之后的位置,也就是 dp[idx+1][c]。
状态转移表示 前面的状态要由后面的状态而来,所以动态规划应该倒过来,由底至上。
底部就是 dp[t.length-1][c],如果在 t.length-1 位置出现了字符 c ,则dp[t.length-1][c] = t.length-1,其余的 25个字符不会再出现,dp值会等于 dp[t.length][c],所以我们建的二维数组应该是 (t.length+1)*26 的,让边界也能进行状态转移,并且 dp[t.length][…] 应该初始化为让我们能够判断这个字符不存在的索引,比如就是t.length。
在遍历 s 中字符的时候,如果发现这个字符在 t 中的索引是 t.length ,则说明 s 并不是 t 的子序列,能够遍历完成则成功。
匹配过程就是直接dp[idx][s.charAt(j)]跳到这个字符所在的索引。
预处理的时间是固定的,并且之后匹配每一个 s 的时间复杂度都是 O(s.length),所以当s数目很多的时候也可以完成匹配。
注意先判断这个字符所在的索引是不是t.length,不是的话索引更新为idx = dp[idx][c]+1用来匹配下一个字符(因为dp[idx][c]已经和这一个字符匹配了),如果没有这个+1一定错。
比特位计数
三种动规都很好理解。
53. 最大子数组和
要边维护最小前缀和一边求答案,不能求出最大、最小前缀和再算差值,因为最小前缀和可能会出现在最大前缀和后面,我就是犯了这个错误一直写不出来。
并且前缀和要初始化为0,并且 curSum 加上当前值之后才能与 minPreSum 相减,因为子数组至少要有一个数。
1 | int ans = Integer.MIN_VALUE; |
第一次接触到 线段树
这个线段树很有意思 ,维护四个变量,合并过程也很有趣
线段树区间合并法解决多次询问的「区间最长连续上升序列问题」和「区间最大子段和问题」
376. 摆动序列
这个动规解释的很好
定义双状态,两个状态之间进行转移,不同于以前见到的只有一个状态。
上升摆动序列
下降摆动序列
1 | var wiggleMaxLength_2 = function (nums) { |
背包问题
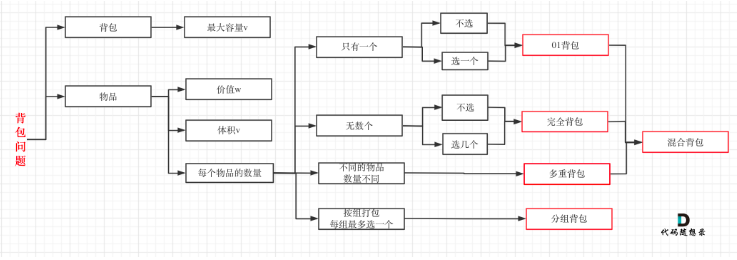
0-1背包问题讲解见 代码随想录
在一维dp中很重要的一点就是遍历的顺序,首先,最外层应该是待放物品,这是最基本的保证物品只取一次的要求,其二,内层循环应该倒序,因为:在dp数组更新的时候是用上一层的左边索引处的值来更新当前层当前索引处的值,如果正序的话,那每个左边索引值都给你改成新值,还是错的,当前索引值有可能是对的么?
上面两个坑我都踩过了,卡哥还是牛。
1 | for(int i = 0; i < weight.size(); i++) { // 遍历物品 |
完全背包问题讲解
01背包内嵌的循环是从大到小遍历,为了保证每个物品仅被添加一次。
而完全背包的物品是可以添加多次的,所以要从小到大去遍历,即:
1 | // 先遍历物品,再遍历背包 |
01背包中二维dp数组的两个for遍历的先后循序是可以颠倒的,一维dp数组的两个for循环先后循序一定是先遍历物品,再遍历背包容量。
在完全背包中,对于一维dp数组来说,其实两个for循环嵌套顺序是无所谓的!
因为dp[j] 是根据 下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的新值就可以了。
对于纯完全背包问题,其for循环的先后循环是可以颠倒的!
但如果题目稍稍有点变化,就会体现在遍历顺序上。
如果问装满背包有几种方式的话? 那么两个for循环的先后顺序就有很大区别了。
416. 分割等和子集
至于上面说到的 “在dp数组更新的时候是用上一层的左边索引处的值来更新当前层当前索引处的值” ,到底什么时候用左边更新当前,什么时候用右边更新当前呢?
还得看题意。
以本题为例:如果设dp[0] = true,慢慢更新到dp[sum]判断是否等于 true ,翻译过来就是用数组里的数能不能叠加到 sum,那很明显从索引0->sum自然就是以左更新右。
此时要用dp左边更新dp右边,所以肯定是先改右边的数再去改左边的数,即逆序。
我也可以这么看:设dp[sum] = true,慢慢更新到dp[0]判断是否等于 true ,翻译过来就是我能不能用 sum 去减数组的数,最终减到0,从索引sum->0自然就是以右更新左。
此时要用dp右边更新dp左边,所以肯定是先改左边的数再去改右边的数,即正序。
1 | class Solution { |
1049. 最后一块石头的重量 II
这个讲的也不错
1 | // 思路: |
518. 零钱兑换 II
纯完全背包问题由于并不限制数组只取一次,所以内外循环没有额外要求,但某些情况除外!因为纯完全背包问题求的是最大价值,多余的排列并不影响这个值,但是影响计数!
不限制数目,所以是一个完全背包问题,但要注意的本题求的是组合数。
做法就是固定硬币的顺序,让外层循环遍历数组 coins 的值,内层循环遍历背包的大小,这样在求出 dp[i]的时候,该金额对应的硬币面额的顺序就固定了,因此不会计算重复的排列。
如 coins = [1,2],对于 dp[3] 的计算,因为先遍历面额 1 再遍历面额 2,所以不会出现2+1的组合,只有1+1+1 和 1+2的组合。
反之,如果两个循环遍历颠倒,外层循环遍历背包的大小,内层循环遍历数组 coins 的值,则因为每个dp[i]都去尝试各个硬币值,一定会出现重复的排列,如coins = [2,3,5],对于 dp[5] = 2+3 和 3+2,这就是区别。
377. 组合总和 Ⅳ
刚好,上一题是组合,这一题考的是排列,很明显,只要更换内外层循环的顺序即可。
外层循环遍历从 1 到 target 的每个值,内层循环遍历数组 nums 的值,外层的每个值作为一个总和计算 dp[i] 时要考虑以 nums 的每一个小于等于 i 的数作为排列的最后一个元素的情况,将这些情况加起来作为当前的排列数。
如:以 nums={2,3,5} 为例,计算 dp[5]时会以 2 为结尾,以 3 为结尾,所以dp[5] = dp[3]+dp[2]。动手模拟下也能发现。
背包总结
背包的递推公式比较容易,难在遍历顺序上,把遍历顺序摸透,才算是真正理解背包。
一维 dp 数组 01背包 只能先遍历物品再遍历背包容量(因为每个物品只有一个),且第二层for循环是从大到小遍历(因为要用dp数组左边的旧值更新当前的值,所以只能从右往左更新)。
一维 dp 数组 纯完全背包先遍历物品还是先遍历背包都是可以的(因为纯完全背包求得是最大价值,求排列还是组合并不影响),且第二层for循环是从小到大遍历(因为每个物品可以取无限次)。
完全背包如果求组合数就是外层for循环遍历物品,内层for遍历背包(固定物品的顺序)。
完全背包如果求排列数就是外层for遍历背包,内层for循环遍历物品(不固定物品顺序)。
打家劫舍
动态规划经典题,有扩展。
关键就在于 考虑这个关键字。
如果偷当前 i 这个房间,则 i-1不能考虑,注意,考虑不代表一定偷,偷不偷由遍历过程中的max来决定,保证取最大值。
也就是 dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
树 dp
目前做到的树 dp 都是用数组作为容器储存状态,就像之前提过的,问题复杂时可以用更多的状态来实现动态规划。
968. 监控二叉树
337. 打家劫舍 III
1 | class Solution { |
股票问题
股票问题常常增加状态的维度
123. 买卖股票的最佳时机 III
这题比较难,很关键的一点就在于一定要定义清楚状态,不能把第一次交易和第二次交易混在一起,第二次交易一定是在第一次交易结束的时候进行的。
300. 最长递增子序列
这题的贪心解法很有意思,也很难想。
贪在让子序列最后一个元素最小,让 minTail[i] 为所有长度为 i 的子序列中最小的尾元素。
1 | class Solution { |
字符串二维 dp
1143. 最长公共子序列
拼多多一面原题
明明718. 最长重复子数组一下就写出来了,这题基本一样写老半天。
这种题就得动态规划做,整那种花里胡哨的就等死吧。
和以前做的题很不一样的是这种匹配问题关键就是这种都是 二维dp。
状态转移的关键不再是判断一维状态是否相等了,而是二维各自的元素是否相等了,一共两种状态。
1 | class Solution { |
72. 编辑距离
72. 编辑距离
编辑距离算法被数据科学家广泛应用,是用作机器翻译和语音识别评价标准的基本算法。
编辑距离是一系列经典题目,很多二维dp题都由编辑距离改编而来,重中之重。
这题的关键在于 虽然说是让 word1 向 word2 靠齐,也就是字面意义的 word2 不能改,但在逻辑上是可以改的,word1 插入一个最合适的数等效于 word2 删除一个数,毕竟在 dp 过程中是肯定不能在word1 显式插入一个数字的。
妈的就倒在这了,只考虑word1删除和替换元素,甚至考虑到如果 word1 比 word2 短就反过来执行程序。
唉,so close。
关键:对两个单词计算编辑距离,插入与删除等价!
这样一来,本质不同的操作实际上只有三种:
在单词 A 中删除一个字符;
在单词 B 中删除一个字符;
修改单词 A/B 的一个字符。
回文 dp
5. 最长回文子串 许多回文题基本都很相似,可以用 dp 做, 也可以用 中心扩展法(双指针法)做,还有 Manacher 算法。
中心扩展法 空间性能比 DP 更好,关键就是 首先回文串要么是偶数长度要么是奇数长度,而区分不同回文串的要点除了回文串的内容,还有就是回文串的中心(这个中心更具体地是指中心在原字符串中所处的位置),因为当回文中心不一样时也算不同的回文子串,计算 回文子串数目 或者 回文子串长度 都是不影响的。
那接下要做的就是遍历所有的回文中心,获得这个中心能向外扩展得到的偶数长奇数长回文子串,故谓中心扩展。当然这里的回文中心是广义的,因为偶数长回文子串肯定是由起始长度为2的回文中心向外扩展而来的。
写法是:
1 | for(int i = 0; i<n; i++) { |
97. 交错字符串
97. 交错字符串 真难阿,好久没遇到写不出来的中等题了。唉悲伤
单调栈
什么时候用单调栈呢?
通常是一维数组,要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置,此时我们就要想到可以用单调栈了。时间复杂度为O(n)。
654. 最大二叉树
图解讲的很清楚
这题用单调栈
边遍历数组边构造树只遍历一次,真的太精妙了。
感觉关键就在于:
1、有大小的比较
2、入栈元素可能是我的右节点,也可能我(栈顶)或者我下面的一些都属于它的左子树。一切都是根据大小的比较。
最难的就是想到边形成单调栈边构造,我一直以为单调栈是生成完了才用,和单调队列一样。
下一个更大元素 I
自己写出单调栈了哈哈
1 | class Solution { |
739. 每日温度
第一次做到存储下标的,之前都是直接存储数,还是看需求的,必须这题的需求就是两个数索引的差。
42. 接雨水
42. 接雨水 一开始我是用类dp法写的,比较简单。
这题的单调栈法很不错,有种一层层往上加的感觉,原理就是栈里保存比栈顶大的,然后遍历过程中遇到比当前栈顶大的,那么对这个栈顶来说就已经是一个坑了,可以装水。
双指针法有点难,关键是只需要知道左右两边比自己高的两个柱子中比较低的一个,所以当左边/右边出现了一个比现在明确的真正意义上的右边/左边最大高度柱子时,当前位置能接的水量也就知道了。
1 | int ans = 0; |
84. 柱状图中最大的矩形
看看我的题解
图
图的遍历 讲的不错。
1 | // N叉树 |
广搜: 广搜的搜索方式就适合于解决两个点之间的最短路径问题。
因为广搜是从起点出发,以起始点为中心一圈一圈进行搜索,一旦遇到终点,记录之前走过的节点就是一条最短路。
当然,也有一些问题是广搜 和 深搜都可以解决的,例如岛屿问题,这类问题的特征就是不涉及具体的遍历方式,只要能把相邻且相同属性的节点标记上就行。
只要BFS只要搜到终点(搜到的一瞬间)一定是一条最短路径,不管有没有障碍。DFS 应该是需要遍历完所有的路径并维护最短路径。
一圈一圈的搜索过程是怎么做到的,是放在什么容器里,才能这样去遍历?
很多网上的资料都是直接说用队列来实现。
其实,我们仅仅需要一个容器,能保存我们要遍历过的元素就可以,那么用队列,还是用栈,甚至用数组,都是可以的。
用队列的话,就是保证每一圈都是一个方向去转,例如统一顺时针或者逆时针。
因为队列是先进先出,加入元素和弹出元素的顺序是没有改变的。
如果用栈的话,就是第一圈顺时针遍历,第二圈逆时针遍历,第三圈有顺时针遍历。
因为栈是先进后出,加入元素和弹出元素的顺序改变了。
那么广搜需要注意转圈搜索的顺序吗? 不需要!
所以用队列,还是用栈都是可以的,但大家都习惯用队列了,所以下面的讲解用我也用队列来讲,只不过要给大家说清楚,并不是非要用队列,用栈也可以。
200. 岛屿数量
flood fill 算法,水漫算法,相当于用每种颜色填充每一个连通块。
200. 岛屿数量 好难
难在想到每次处理一个岛屿,只处理所有连成一片的 1 。
广搜难在需要注意到:是加入队列时进行标记访问过这个点,而不是出队的时候进行标记。
这取决于我们对 代码中队列的定义,队列中的节点就表示已经走过的节点。 所以只要加入队列,立即标记该节点走过。
并查集解法
已经完全解析了,看注释吧。
1 | class UnionFind { |
并查集
并查集常用来解决连通性问题。
大白话就是当我们需要判断两个元素是否在同一个集合里的时候,我们就要想到用并查集。
并查集主要有两个功能:
将两个元素添加到一个集合中。
判断两个元素在不在同一个集合
并查集理论基础 讲的不错
1 | int n = 1005; // n根据题目中节点数量而定,一般比节点数量大一点就好 |
注意,join 函数中前三行和 isSame 函数是重复的,但这三行绝对不能用通过调用 isSame 函数来替换,因为下一行的 father[v] = u 表示的意思是让 v 的 根 指向 u的 根,这样才能通过单向的连接就能表示两个元素的相连。否则单单 father[v] = u 的意思就是让 v 指向 u ,比如:
1 | join(1, 2); |
这是用 isSame 替换,此时无法表示 1 与 3 在一个集合里。
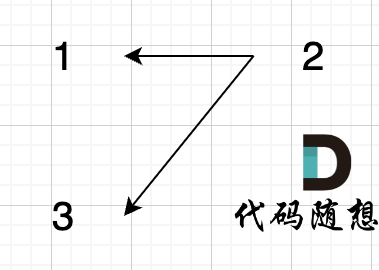
这是不用 isSame 替换,此时可以表示 1 与 3 在一个集合里。
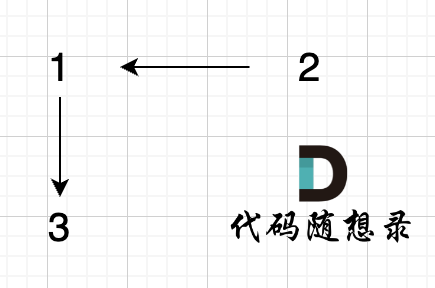
join(u, v) 的含义就是 v 的根(或者叫头)指向 u 的根(或者叫头)。这点和上面的那个易错点是很关连的。
还有:路径压缩 // 验证过了
路径压缩会在寻根的漫长过程中,把这条路径上的所有非根节点的父节点全都设为最前端的根节点,只要这条路径跑一次,基本都会重设父节点,这些子节点都会直接挂载到根节点下面。
注意看:无论使用并查集模板里哪一个函数(除了init函数),都会有路径压缩的过程(因为里面都调用了 find 函数),第二次访问相同节点的时候,这个节点就是直连根节点的,即 第一次访问的时候它的路径就被压缩了。
路径压缩后的并查集时间复杂度在O(logn)与O(1)之间,且随着查询或者合并操作的增加,时间复杂度会越来越趋于O(1)。
在第一次查询(find)的时候,相当于是n叉树上从叶子节点到根节点的查询过程,时间复杂度是logn,但路径压缩后,后面的查询操作都是O(1),而 join 函数 和 isSame 函数里涉及的查询操作也是一样的过程。
拓展
在「路径压缩」讲解中,我们知道如何靠压缩路径来缩短查询根节点的时间。
其实还有另一种方法:按秩(rank)合并。
rank表示树的高度,即树中结点层次的最大值。
为防止两颗树合并后整棵树的高度变的更高,一定是 rank 小的树合入 到 rank大 的树(比较矮的树合入比较高的树),这样可以保证最后合成的树rank 最小,降低在树上查询的路径长度。
按秩(rank)合并不需要路径压缩,因为一旦做路径压缩,rank记录的高度就不准了,根据rank来判断如何合并就没有意义。
其实我们在优化并查集查询效率的时候,只用路径压缩的思路就够了,不仅代码实现精简,而且效率足够高。
按秩合并的思路并没有将树形结构尽可能的扁平化,所以在整理效率上是没有路径压缩高的。
1 | int n = 1005; // n根据题目中节点数量而定,一般比节点数量大一点就好 |
拓扑排序
还是容易理解的
字典序算法
字典序算法详解 讲的挺好的。
字典序算法用来解决这样一个问题:给定其中一种排列,求基于字典序的下一种排列。
比如给定一种排列为 abc,则其基于字典序的下一种排列为 acb。
要求下一种排列既要比原排列大,又不能有第三种排列位于他俩之间。即下一种排列为大于原排列的最小排列。
其实我们总体目标就是把一个递增序的123456转为递减序的654321【这里是从左往右看的】
以输入为 3 2 5 8 7 6 4 为例,字典序算法的步骤:
1、从右往左看,寻找最先出现的两个从右往左看呈递减趋势的数字,这里就是5 8,称5为左邻,8为右邻。【右邻8及其右边已经呈我们要的递减了,没法再在这边操作了】
2、重新从右往左找第一个比左邻5大的数(这里一定是找大于它的数,换一个等于的数有啥用),因为我们要用一个较小的数去和5换。这样换完之后才能小一点。这里我们找到6,将它和5换,则得到 3 2 6 8 7 5 4,左邻位置现在是6。【这里我们注意到8 7 5 4和原来一样是递减的,原因就是因为6是第一个大于5的】
3、将左邻位置(也就是现在的6)后面的所有数字重排序成递增的,得到3 2 6 4 5 7 8,这里我们只要使用双指针一直头尾交换就可以啦。
还是很简单滴。注意第一步如果没有这样的两个数说明已经全局递减的,这时候直接跳到第三步,形成一个循环。
疑难
105 106从前序与中序遍历序列构造二叉树 迭代法很恶心
491. 非递减子序列 回溯去重
这个回溯去重真看不懂
295. 数据流的中位数 题简单,但是第一次见到用TreeMap,可以再了解下
373. 查找和最小的 K 对数字 这题的二分查找可能有点难了
MySQL
题
给学生表、课程成绩表,求不存在01课程但存在02课程的学生的成绩
太难了呀
select s.sid, s.name, sc.cid, sc.score
from studeng s join score sc on s.sid=sc.sid and sc.sid=’02’
where not exists (select 1 from Score where Score.sid=s.sid and Score.cid=’01’)
select s.sid, s.name, sc.cid, sc.score
from
student s left join score as sc1 on s.sid=sc1.sid and sc1.cid=’01’ left join score as sc2 on s.sid=sc2.sid and sc2.cid=’02’
where sc1.cid is null and sc2.cid is not null;
给定一个学生表 student_score(stu_id,subject_id,score),查询总分排名在5-10名的学生id及对应的总分
WITH StudentTotalScores AS (…): 定义 CTE(子查询 (Common Table Expressions, CTE),计算每个学生的总分。
RANK()函数是一种窗口函数,用于生成一个特定排序的序号。它与OVER子句结合使用,以指定排名的排序依据。
RANK()函数用于生成排序结果中的排名。不同于ROW_NUMBER(),它会处理并列的情况。例如,如果有两个记录的得分相同,那么它们会得到相同的排名,下一名将跳过。
OVER子句用于定义窗口函数的分区和排序方式,在你的例子中,它指定了如何排序生成排名:
窗口函数应用于ORDER BY total_score DESC:按总分从高到低进行排序。
RANK() OVER (ORDER BY total_score DESC) AS rank:
RANK(): 生成排名。
OVER (ORDER BY total_score DESC): 按总分从高到低排序来计算排名。
AS rank: 给生成的排名列取名为rank。
WITH StudentTotalScores AS (
SELECT
stu_id,
SUM(score) AS total_score
FROM
student_score
GROUP BY
stu_id
),
RankedStudents AS (
SELECT
stu_id,
total_score,
RANK() OVER (ORDER BY total_score DESC) AS ranking
FROM
StudentTotalScores
)
SELECT
stu_id,
total_score
FROM
RankedStudents
WHERE
ranking BETWEEN 5 AND 10;
除了这种声明子查询为某个表的with方式,还可以使用
1 | FROM ( |
在from的时候用小括号命名别名为表T
1934. 确认率
有个问题待解决,当两个相同的表leftjoin似乎会产生类笛卡尔积,实际上是由于连接条件不唯一导致的
原来join是(以left join为例),此刻选择两条记录,如果满足on后面的条件,就将右边的记录接在左边后面成为一条新纪录作为结果集之一,并且如果对一条左边记录来说,右边没有任何一条符合则会生成一条【左边记录-null】的新纪录。所以以后连接条件一定要唯一,否则容易拿不到自己想要的结果。
SELECT *
FROM table1 AS alias1
LEFT JOIN table2 AS alias2
ON alias1.column = alias2.column;
会从 table1 中获取所有记录,并根据 ON 条件与 table2 中的记录进行匹配。如果匹配成功,返回匹配的记录;如果匹配不成功,则返回 table1 的记录,并用 NULL 填充 table2 的列。
IFNULL(expression, alt_value)
如果第一个参数的表达式 expression 为 NULL,则返回第二个参数的备用值。
IF函数根据条件的结果为true或false,返回第一个值,或第二个值
IF(condition, value_if_true, value_if_false)
ROUND() 函数用于把数值字段舍入为指定的小数位数。
ROUND(column_name,decimals) decimals:可选。规定要返回的小数位数decimals 甚至可以是0、负数,用于对小数点左边进行四舍五入。
COUNT:是对记录进行汇总,即计数记录数
SUM:是对符合条件的数值列字段进行求和
SUM函数内部设置筛选条件
sum( action = ‘confirmed’ ) sum不止可以用于字段
每个Price与25对比后的判断结果,小于25,判断为False,用数字0表示;大于25,判断为True,用数字1表示;
可以发现,虽然判断结果为False,但仍然是一条记录,所以前两行虽然判断结果为0,但是 count(price>25)列仍填充1(对count来说只要不为null就计数)
price>25为False,即0,相当于sum( 0 ) 结果仍然是0
也可以在sum内部写if条件sum(if(tb2.action='confirmed',1,0)
按照这样的理论,sum绝对不止局限在字段,可以理解为对每条记录可以进行一样计算,并为其总和,比如我可以在sum中进行两个字段的相乘。
可以考虑使用AVG函数,需要注意的是AVG函数是可以写条件判断的。
AVG(c.action=’confirmed’) 应该也是判断为False,用数字0表示,判断为True,用数字1表示,然后除以总行数
布尔表达式在MySQL中的行为
在MySQL中,布尔表达式(如 c.action = ‘confirmed’)在数值上下文中会被隐式转换为数值:
真(TRUE)被转换为 1。
假(FALSE)被转换为 0。
因此,表达式 c.action = ‘confirmed’ 对于每一行来说,要么是1(如果 action 是 ‘confirmed’),要么是0(否则)。
1251. 平均售价
1633. 各赛事的用户注册率
两个表没必要连接,但主表需要另一个表的某个信息,此时就是子查询嵌套,不是连接了
在select里面用**(select count(1) from users)**表示从user表查到的行数,直接就用了。
1 | select |
mysql order排序 默认是升序
多字段排序需要各自分别定义升降序
比如
SELECT * FROM students st ORDER BY st.sAge DESC, st.sGrade ASC;
并且按字段先后顺序排优先级,这里就先Age降序,然后Grade 升序
用distinct来返回不重复的用户名select distinct name,id from user, 去重
1211. 查询结果的质量和占比
判断字段是否为null 要用 字段-IS NOT NULL,不能用!=
1193. 每月交易 I
我们在用Mysql抽取数据时候,经常需要按照天、周、月等不同的粒度对数据进行分组统计。而我们的时间可能是“2017/12/5 0:0:0”这种准确的时间。所以在进行分组之前我们需要对时间进行一下处理。
DATE_FORMAT是MySQL内置的一个函数,作用是以不同的格式显示日期/时间数据。具体的语法如下:
DATE_FORMAT(date,format),其中
date:合法的日期。format:规定日期/时间的输出格式
按天统计:select DATE_FORMAT(start_time,‘%Y%m%d’) days
按周统计:select DATE_FORMAT(start_time,‘%Y%u’) weeks
按月统计: select DATE_FORMAT(start_time,‘%Y%m’) months 这样的会转化成字符串”201812”
其中年的Y换成y则只会输出后两位,比如2018的18,m换成M则变成月份英文单词,d同理。
这题要输出成【2018-12 】这样的格式,所以使用date_format(trans_date,’%Y-%m’)
或者也可以left(trans_date, 7) 从左侧取七位
550. 游戏玩法分析 IV
被子查询狠狠坑了,就是基础不好。(时间加一天不会,多表联查不知道,)
草泥马的,我以为 select from只能从一张表查,我真服了!
原来可以用逗号分隔查两张表(这样是笛卡尔积连结),比如
1 | select Activity.player_id as player_id |
能够直接求出某列去重后的元素
select count(distinct player_id) from activity
count(distinct Activity.player_id) 直接就是去重后的行数
仔细看这里的区别, 第一个多表联查result, Activity,所以只要count(distinct Activity.player_id)就行,第二个只有result,所以要(select count(distinct player_id) from activity)
1 | -- select round(result.cnt/ count(distinct Activity.player_id),2) as fraction |
1378. 使用唯一标识码替换员工ID
join(外连接)
1.inner join,内连接,显示两个表中有联系的所有数据;简写成join,如果一边缺了会自动重复。
2.left join,左链接,以左表为参照,显示所有数据,右表中没有则以null显示
3.right join,右链接,以右表为参照显示数据,,左表中没有则以null显示
比如这题就要用到left/right JOIN1378. 使用唯一标识码替换员工ID因为要留NULL。
关键字 on
数据库在通过连接两张或多张表来返回记录时,都会生成一张中间的临时表,然后再将这张临时表返回给用户。
在使用 left/right jion 时,on 和 where 条件的区别如下:
1、 on 条件是在生成临时表时使用的条件,它不管 on 中的条件是否为真,都会返回左边表中的记录。
2、where 条件是在临时表生成好后,再对临时表进行过滤的条件。这时已经没有 left join 的含义(必须返回左边表的记录)了,条件不为真的就全部过滤掉。
使用 inner join 时on和where是一样的
mysql的left join和inner join的详细用法 这篇讲得好
1280. 学生们参加各科测试的次数
交叉联结(corss join):
使用交叉联结会将两个表中所有的数据两两组合
写join时默认就是 cross join ,这东西真的很重要,有时候为了获得某几列的所有组合就要用这个东西。
比如难题
1 | 官解的写法也能学到些东西 |
注意 USING (student_id,subject_name)意思是连结的用student_id subject_name这两列,也就是两个表有相同名称的这两列时可以这么用,完全可以用on代替,但是这里代替的写法应该是
ON stu.student_id = ex.student_id AND sub.subject_name = ex.subject_name 注意中间的and。
还发现 GROUP BY 、ORDER BY 都可以选一列以上
1 | SELECT |
570. 至少有5名直接下属的经理
having count(Report.Id) >= 5 应该也是返回临时表
函数合集:
计算字符串中字符数的最佳函数是 CHAR_LENGTH(str)
另一个常用的函数 LENGTH(str) 返回字符串 str 的字节数,如果包含特殊字符(某些字符包含多于 1 个字节),结果可能和预期不太一样
COUNT 想计数某个字段重复次数,先按这个字段group,然后count(另一个字段),这题就用到了,比如:想计算customer_id下有几个visit_id,就GROUP BY customer_id然后 COUNT(visit_id)
| visit_id | customer_id |
| 4 | 30 |
| 6 | 96 |
| 7 | 54 |
| 8 | 54 |
1581. 进店却未进行过交易的顾客
count() 是一个聚合函数,函数的参数不仅可以是字段名,也可以是其他任意表达式,该函数作用是统计符合查询条件的记录中,函数指定的参数不为 NULL 的记录有多少个。COUNT(visit_id)是统计表中,visit_id 字段不为 NULL 的记录有多少个
时间计算的函数:
datediff(日期1, 日期2):很重要
得到的结果是日期1与日期2相差的天数。
197. 上升的温度
1 | SELECT w1.id |
MySQL 知识点
count(age > 20 or null) 最好不要用 or null 这种写法,用count(if(age > 20,1,null)或者 sum(age > 20)比较好。注意这里之所以可以sum(age > 20)因为对布尔表达式会默认转为0、1。
判断字段空:只有name 为null 的时候 ISNULL(exp) 函数的返回值为1 ,空串和有数据都为0;
也可以 name is not null; 或 name is null;
排序:order by 排序字段 asc(默认,还可选desc)
去重:根据某些字段的去重查询(不考虑查询其他字段)
select distinct 字段 from table
或者 group by 也可以去重
select c_name,c_year,c_month from table
group by c_name,c_year,c_month
别名
列别名:SELECT 字段 [AS] 别名(AS关键字是可选的,别名如果有空格最好用单引号括起来)
组合字段并使用别名
CONCAT_WS(‘, ‘, lastName, firstname) [AS] ‘Full name’
ORDER BY,GROUP BY和HAVING子句中可以引用这些别名,不能在WHERE子句中使用列别名。
1 | SELECT customerName, |
select 命令执行流程
sql查询语句执行逻辑顺序:
1 | (9) SELECT |
但注意 sum/count(distinct 某列)是能发挥distinct作用的,因为此时distinct是作为聚合函数的参数一块执行的。
但注意日期格式化data_format之后的字段别名可以用在group by中,因为涉及到SQL 的执行流程,在 SELECT 语句执行前会经历:语义校验(词法分析) ->语法校验(语法分析)->(构建)语法树->优化器->执行器。本例的 date_formate 就是在语法树之前就编译好了的,所以最后丢给执行器执行时就能使用前面的编译内容去得出结果。【select date_format(trans_date,’%Y-%m’) as month…from…group by month】
MySQL 日期函数
mysql日期函数
now() 当前日期和时间
curdate() 当前日期
date(某个日期时间) 获取日期或日期时间的日期部分
time() 仅时间
date_format()将日期和时间转为指定格式字符串
between…and(推荐)判断某个时间是否在某个时间范围内SELECT * FROM k_student WHERE create_time between '2019-07-25 00:00:33' and '2019-07-25 00:54:33'
也可以用大小于号
datediff(expr1, expr2)用于计算两个日期之间的天数差。
expr1 和 expr2 是两个日期表达式。expr1 表示结束日期,expr2 表示起始日期。
DATEDIFF 函数返回的是 expr1 与 expr2 之间相差的天数。
最小天数加一天
DATE_ADD(MIN(event_date), INTERVAL 1 DAY)
DATE_SUB(MIN(event_date), INTERVAL 1 DAY)
另一个关于时间计算的函数是:
timestampdiff(时间类型, 日期1, 日期2)
这个函数和上面 datediff 的正、负号规则刚好相反。
日期1大于日期2,结果为负,日期1小于日期2,结果为正。
在“时间类型”的参数位置,通过添加“day”, “hour”, “second”等关键词,来规定计算天数差、小时数差、还是分钟数差。
在 SQL 语句中,对字段加单引号的情况通常是为了区分字符串常量和列名,而不加单引号的情况通常是用于列名或保留字。
何时加单引号
字符串常量:在条件语句中如果要对一个列进行字符串比较或使用字符串常量,需要用单引号。例如:’approved’, ‘active’ 等。
日期常量:日期常量也需要用单引号。例如:’2023-12-08’, ‘2024-01-01’ 等。
字符型数据的插入:在插入字符型数据时需要用单引号。例如:
INSERT INTO users (name, status) VALUES (‘John Doe’, ‘active’);
何时不加单引号
列名:列名通常不需要用单引号。例如:state, amount 等。
保留字:保留字在某些情况下可能会被错误识别,但如果它们明确指向数据库中的列或表,则不需要单引号。为了避免冲突,可以用反引号(MySQL)或双引号(标准 SQL)来引用,例如:state, `table` 等。
数值型常量:数值型数据在 SQL 语句中无需用单引号。例如:100, 0, 3.14 等。
1 | count 的 case 写法 |
子查询
子查询能否使用外部查询的字段取决于其位置和类型:
- 具有独立上下文的子查询(如作为表达式使用)不能使用外部查询的字段。
- 在 FROM 子句中的子查询可以是独立的,但也可以通过 JOIN 关联外部查询的字段。
- 关联子查询(例如在 WHERE 子句和 SELECT 子句中的子查询)通常会使用外部查询的字段。
1、作为表达式使用:
1 | select contest_id , round(count(user_id) * 100/ (select count(*) from users), 2) as percentage |
子查询(select count(*) from users)为主查询中的表达式提供数据,甚至可以 (select count(distinct name) from users) 查询users 表中的用户总数。
这种子查询不能使用外部查询的字段,因为它在单独的、独立的上下文中运行。
看这里甚至在where中的datediff里也用了子查询作为一个表达式,也就是这题 1321. 餐馆营业额变化增长
1 | select visited_on, amount, round(amount/7, 2) as average_amount |
2、在 FROM 子句中作为一个临时表使用:
子查询可以作为一个临时表来使用,并在主查询中引用,这里的引用不局限于单表引用,也可以join其他表。
1 | select t.contest_id, t.avg_score |
这里子查询将 Results 表按照 contest_id 分组并计算 avg_score,然后主查询从这个子查询结果中过滤 avg_score 大于 50 的记录。
3、在 WHERE 字段 in、EXIST 或 HAVING 子句中使用:
子查询很常用的一个场景是在 WHERE 或 HAVING 子句中,通常用于提供过滤条件。
1 | SELECT contest_id, user_id |
WHERE EXIST 这种子查询还经常会使用外部查询的字段。
1 | SELECT u.user_id, u.name |
4、在 SELECT 子句中使用(SELECT 子句的结果作为一列):
1 | select user_id, |
这里子查询还用了外部查询的字段作为子查询内部的过滤条件,甚至子查询发生在外部查询的from子句前面。
由于子查询需要嵌套并执行多次,因此在性能方面要特别注意。如果你的数据集非常大,频繁的子查询可能会导致查询性能下降。在可能的情况下,使用 JOIN 操作或优化索引策略可能会更有效。
在 SELECT 子句中使用的这种子查询,如果子查询结果集是空集,那么外部查询对该结果的处理通常为返回 NULL。
SELECT (SELECT Salary FROM Employee WHERE Salary = 10000) AS Result;
结果就是:
Result
NULL
在 SQL 查询中,当在 SELECT 子句中使用子查询时,通常要求子查询返回的结果集只有一行。如果子查询返回多行而没有适当处理,会导致 SQL 查询执行失败。
当在 SELECT 子句中使用子查询时,情况有两种:
子查询返回零行或一行:
这是期望的标准情况。
当子查询返回零行时,外查询结果为 NULL。
当子查询返回一行时,外查询结果为该行的值。
子查询返回多行:
这会导致 SQL 查询执行失败,抛出错误,如 Subquery returns more than 1 row。
在 SQL 中,子查询返回多行时不能直接用在 SELECT 子句中。这是因为SELECT子句期望的是标量子查询(即返回单一值的子查询)。如果子查询返回了多行数据,SQL 查询将会失败,并报错类似于 Subquery returns more than 1 row。
其实,如果子查询返回空集,那么外部查询就可以把它视为NULL。这个在其他情况待定,但基本没问题。
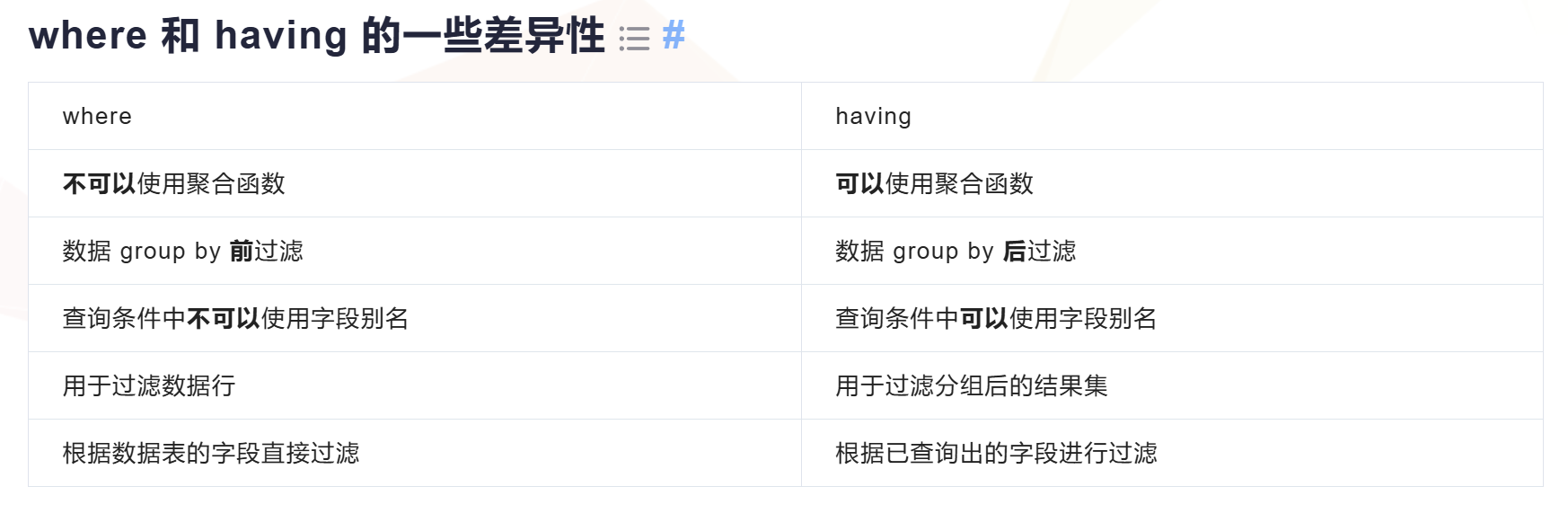
having where
官网中明确表示
可以在group by、order by、having子句中使用别名。
不可以在where中使用别名。
having是执行select前的最后一步
注意:在 HAVING 子句中不允许使用聚合函数和一个原始字段进行比较,因为 HAVING 是在分组后进行过滤的,而这个分组后的过滤无法访问原始的非聚合字段。
having只能使用GROUP BY分组之后的聚合结果字段,也就是每一组数据的统计数据,比如SUM、AVG、MAX、MIN 和 COUNT 等,这些函数计算的结果就是聚合后的结果。这个分组的名字也可以用(GROUP BY 子句中的分组字段)。
如果你试图在 HAVING 中使用一个原始数据的字段,则会出现错误。因为这些字段已经被聚合,或者说这些字段在分组后已经不再代表原始的单个数据行,而是代表整组数据的聚合结果。
当SQL语句中使用了group by关键字后,select后面除了聚合函数,就只能是group by后面出现的字段。
包括select也是只能用这几个字段 这篇文章写得好。
WHERE 用于在数据分组和聚合之前过滤记录。换句话说,它作用在 GROUP BY 语句之前,因此不能使用聚合函数。
HAVING 用于在数据分组和聚合之后过滤记录,通常与 GROUP BY 一起使用。HAVING 可以使用聚合函数。
使用 WHERE 条件
使用 WHERE 来过滤记录时,不能直接基于聚合函数(如 SUM)进行过滤(也就是说不能用聚合函数),而只能过滤分组前的记录。例如,我们只能在数据分组前过滤 sale_amount 小于 50 的记录:
1 | SELECT product_id, SUM(sale_amount) as total_sales |
这个查询会首先过滤掉 sale_amount < 50 的记录,然后对剩下的记录进行分组并计算总销售额。
使用 HAVING 可以也只能基于聚合函数的结果进行过滤(不能再用原始字段)HAVING SUM(sale_amount) > 200;
join
JOIN … ON … 默认是 INNER JOIN,与显式的 INNER JOIN 等价。
明确的 CROSS JOIN 或使用逗号 FROM table1, table2 会生成两个表所有行的笛卡尔积。
INNER JOIN 是在 ON 条件过滤后的联结,而逗号分隔的 FROM(from table1,table2) 是生成笛卡尔积,然后(可选)通过 WHERE 子句进行过滤可能可以达到类似 INNER JOIN 的效果。
注意:只要是同一张表与自身进行连接,无论使用 LEFT JOIN、RIGHT JOIN、INNER JOIN 或 CROSS JOIN 等不同的连接方式,都可以称之为自连接(Self Join)。
自连接的关键点在于,同一张表在查询中被引用多次。具体的连接类型只是决定了数据的匹配方式和返回结果的内容。
自连接指的是同一张表在查询中被引用多次,并以不同的别名进行关联。
自连接用途广泛,可以用于处理记录间亲缘关系、比较同表内记录(用的很多)等场景。
limit
limit N,M : 相当于 limit M offset N , 从第 N 条记录开始, 返回 M 条记录
注意,这里两种写法是相反的意思。以后就用limit M offset N比较清晰一些。
SELECT * FROM table_name LIMIT offset, limit;
limit带两个参数时即 limit N,M,偏移N,限制M条
SELECT * FROM table LIMIT 5,10; // 检索记录行 6-15
如果只给定一个参数,它表示返回最大的记录行数目,即LIMIT N返回从0开始N条:
SELECT * FROM table LIMIT 5; // 检索记录行 1-5
WITH 子句
WITH 子句也被称为 “公用表表达式”(Common Table Expression, CTE)。它的主要作用是提高代码的可读性和重用性。WITH 子句允许您定义一个临时的、命名的结果集,可以在后续的 SELECT、INSERT、UPDATE 或 DELETE 语句中使用。
1 | WITH t AS ( |
这段代码定义了一个名字叫 t 的临时结果集。
窗口函数
MySQL 8.0 版本中可以使用窗口函数,它很像分组函数却又区别于分组函数,在使用group by后每组只有一个结果,而窗口函数不论是否分组都是一行一个结果。窗口函数不对数据进行分组,而是按照窗口划分,计算与当前窗口的聚合值,并将计算结果返回给这个窗口的每一行。
MySQL 窗口函数 这篇讲的很清楚。
窗口函数允许您在不通过 GROUP BY 聚合的情况下,在查询结果集中计算某些聚合值。窗口函数通常与 OVER 子句一起使用,它指定了窗口的划分方式(即如何分组数据)。
COUNT(*) OVER(PARTITION BY employee_id) AS count_over
OVER(PARTITION BY employee_id) 指定了窗口分组方式,即按 employee_id 划分数据。
COUNT(*) 对这个划分得到的分组进行聚合,对这个分组进行计数。
AS count_over 给这个计算结果列起了一个别名叫 count_over。
1789. 员工的直属部门 这里之所以要这么做是因为我既需要分组得到count,我又想要不分组时候的原字段。(因为group之后非group字段就消失了)
字符串函数
字符串转换为大写,可以使用UPPER函数
SELECT UPPER(‘hello world’) AS UpperCaseString;
– 输出:HELLO WORLD
要将字符串转换为小写,可以使用LOWER函数
SUBSTRING(column_name, start, length):从列的值中提取一个子串,从指定的起始位置开始,直到指定的长度。
SUBSTRING(name, 1, 1) 拿到name的子串,从位置1开始长度为1的子串。
都可以用来拼接字段
CONCAT(UPPER(SUBSTRING(name, 1, 1)), LOWER(SUBSTRING(name, 2))): 将首字母(大写)和其余部分(小写)进行拼接,得到所需格式的姓名。
CONCAT_WS(separator,str1,str2,…))函数表示使用指定的分隔符 separator 连接多个字符串,分隔符为 NULL 则返回 NULL。
超牛的将多行的字符串按分组整合成一个字符串,必须配合group使用。
1 | GROUP_CONCAT( |
1 | select sell_date, count(distinct product) as num_sold, group_concat(distinct product order by product asc) as products |
INSTR()
INSTR(str, substr)函数用于返回子串 substr 在字符串 str 中第一次出现的索引位置,没有找到子串时返回 0。
另外,LOCATE(substr,str)函数也可以用于返回子串 substr 在字符串 str 中第一次出现的索引位置,和 INSTR(str,substr) 函数唯一的不同就是参数的顺序相反。
MySQL 十大常用字符串函数 讲的挺好。
正则表达式
在正则表达式中,一些字符具有特殊意义,比如 .、*、+、?、^、$、(、)、[、]、{、}、| 等等。如果你想要匹配这些字符本身,需要进行转义,即在这些字符前面加一个反斜杠 \。
由于反斜杠\本身也是特殊字符需要转义,而字符串又以 \ 作为转义符,所以在字符串中表示反斜杠时需要双写象征一个反斜杠,即我们需要使用 \\ 来表示一个反斜杠。
在正则表达式中,\s表示匹配任何空白字符,包括空格、制表符、换页符等。在正则表达式的语法中,这是一个预定义字符类。
同理在正则表达式内,匹配空白字符需要使用 “\s”。
在正则表达式中,方括号 [] 定义字符类,字符类是一个特殊的表示法,用于匹配方括号内任意一个字符
[abc] 匹配 ‘a’、’b’ 或者 ‘c’ 中的任意一个字符。
[0-9] 匹配任意一个数字。
字符类内的大多数字符不具备特殊意义,即它们被视作字面量字符,因此在字符类内不需要转义。例如,. 在字符类外表示任意字符,但在字符类内 [.] 就只表示字面上的一个点号。
元字符在字符类内部的处理 应该只需要考虑这两个
1 | 反斜杠是转义字符,其本身需要转义。不论在字符类内外都需要转义。 |
1 | 元字符(Meta Characters) |
delete语句
一般是 delete from tableName where
注意:为了 SQL 语法和执行流程中的一致性,在删除操作中直接查询同一张表是不允许的。
这里理解下派生表(Derived Table):派生表即子查询生成的一块临时数据集,如这里的 select min(id) id from person p2 group by email 生成的临时数据集。
派生表只在查询执行过程中生存,并且只在此次查询范围内有效。
同样的:这个也是一个派生表,并且由于多加了外层select就”避免“了同时删除和查询同一张表?
具体来讲,当我们在一个查询中既要删除数据又要查询数据时,直接在删除子句 (DELETE) 中操作和查询同一个表可能会引发未定义的行为或者错误。通过使用额外的一层 SELECT,可以有效地避免这些情况。这一层 SELECT 生成了一个派生表,用于隔离修改和查询操作。【有点玄乎,先这么理解吧,得靠外层的select的派生表才能隔绝】【额外的 SELECT 创建了一个派生表,从而建立起了一种逻辑上的数据隔离。这样,不会因为删除操作进行时表的数据变化而影响到查询结果。】
在某些数据库管理系统中,一边查询一边删除同一个表可能会导致死锁或其它并发问题。通过这种迂回查询,避免了直接操作同一张表的问题,从而提高了操作的安全性。
外层 t 的 SELECT 包装了一层将其命名为 t 从而创建了派生表,这样可以确保后续语句引用此子查询结果。而非直接行操作。
派生表 t 的数据在子查询执行的一开始就已经确定了,它不会随着对表 person 的后续操作而变化。
1 | SELECT t.id |
196. 删除重复的电子邮箱 重要的delete题。
1 | DELETE p1 FROM Person p1, |
这种DELETE方式很陌生,竟然和SELETE的写法类似。它涉及到t1和t2两张表,DELETE t1表示要删除t1的一些记录,具体删哪些,就看WHERE条件,满足就删;
UNION和UNION ALL
UNION和UNION ALL 具有不同工作机制:
UNION:默认会对合并的结果集进行去重操作,因此在UNION中每个子查询的ORDER BY子句必须放在整体查询之外,因为在去重之前的排序操作是无意义的。ORDER BY子句在使用UNION时应该对最终合并、去重后的结果进行排序。
UNION ALL:则不进行去重操作,直接合并所有结果集。因此,每个子查询的ORDER BY子句可以保留在自己的子查询内部,因为UNION ALL是直接将所有结果集按照子查询的顺序合并,保留各自的排序。